简介
有一棵树,其树上的每个节点有一个值,且每个节点的这个值都大于等于(小于等于)其父亲上的值。
对于一个基本的堆,它可以支持:插入一个元素,输出最大(小)值,删除最大(小)值。
堆有很多种类,如对顶堆、斐波那契堆……但在这篇博客中,让我们关注一个最基本的堆:二叉堆。
二叉堆
对于二叉堆而言,它是一颗二叉树。
每个节点的这个值都大于等于(小于等于)其父亲上的值
而对于这颗二叉树而言,树根就是它最大(最小)的元素!
为了方便,接下来都会是一个大根堆
还记得吗?对于一个堆,它需要有一些基本的操作:插入一个元素,输出最大值,删除最大值。让我们来一个个的解决吧。
姆好吧……或许在这之前,我们先来看一看怎么存储一颗二叉树吧!
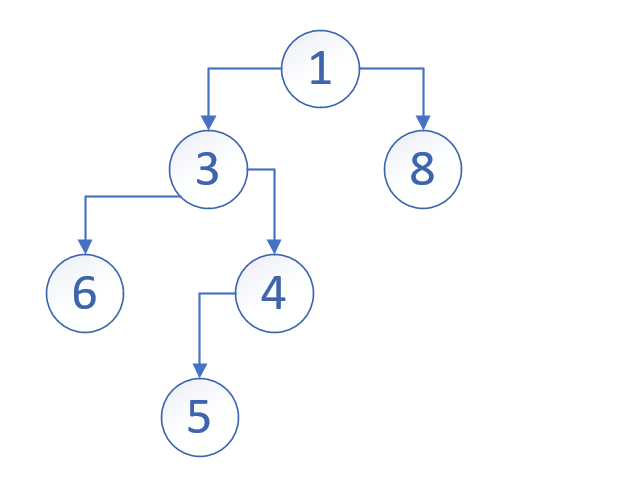
存储
我们线想想一棵二叉树的节点需要存储些什么:
父亲
左子节点
右子节点
或许你会想到数组存子节点、指针、广义表、图……但,在二叉树中,其实都有点麻烦了。毕竟二叉树有个很强的性质:它只有两个子节点!
不知道有没有注意到…数字中就有一种能自然两两配对的东西?不要想复杂了,那便是:奇数和偶数!
对此,我们不妨把所有左节点都存在偶数位置,所有奇数节点都存在奇数位置。并且,当左节点为2 k 2k 2 k 2 k + 1 2k+1 2 k + 1
但是……或许我们也不需要?让我们注意:2 k 2k 2 k k k k ∗ 2 *2 ∗ 2
而子节点则直接2 k 2 \frac{2k}{2} 2 2 k 2 k + 1 2 \frac{2k+1}{2} 2 2 k + 1 1 2 \frac{1}{2} 2 1
对此我们得出了一种如下的存储方式:k k k 2 k 2k 2 k 2 k + 1 2k+1 2 k + 1 k 2 \frac{k}{2} 2 k
最大值
这是最简单的一个了。正如我们见到的,它根节点的元素一定是最大的那个。节点的这个值大于等于其父亲上的值 ,告诉我们:如果除根节点外有一个比根更大的值,那么这条性质必然会被违反!
1 2 3 4 ValueT top () return m_data[1 ]; }
插入
我们不妨假设现在已经有一个合法的堆。我们要向其中插入一个元素的话,直接找到合法位置并不是那么容易。对此,我们不妨破坏堆的一些性质,然后再慢慢的恢复它。
那该破坏哪条呢?
让它不是个二叉树? 敲
让它不是个完全二叉树?不是不行,但是把一颗不完美的二叉树变成完美二叉树同时保持大小关系是很难的,要分割,旋转,跳跃,我闭着眼
那我们只能勉为其难的破坏大小关系了。
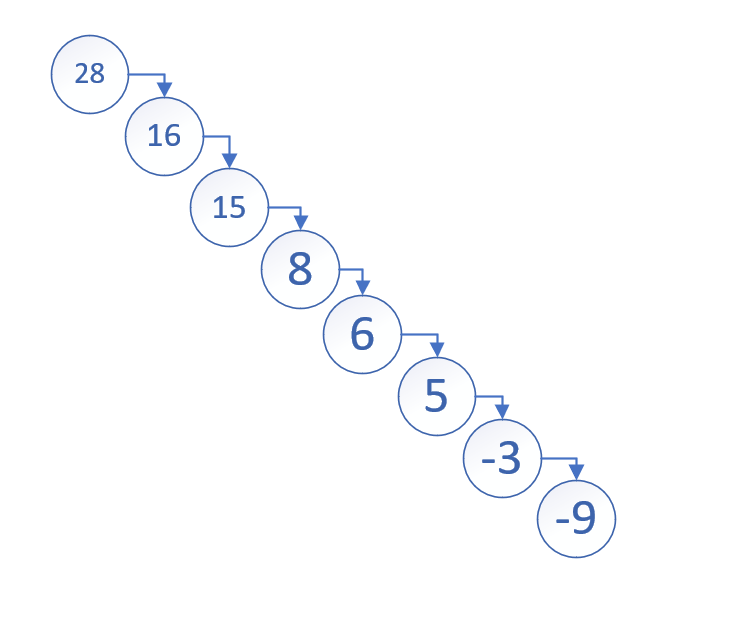
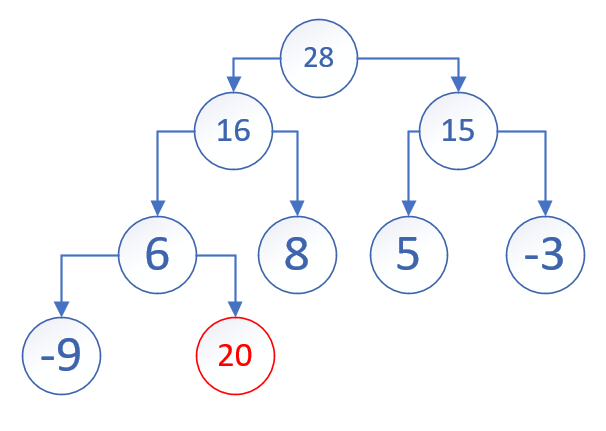
那……该插在哪呢?要让它保持一颗完美二叉树,只能插在最后一层的最右端。恰巧的是,我们发现这正好对应着向数组末尾再加入一个元素!
(为什么呢?该树是满的,所以数组中并没有空位。因此最后一层最后面那个节点一定是下表最大的。其上方所有节点都是它的二分之一以下,左边的2 k 2k 2 k
m_data.push_back(data);
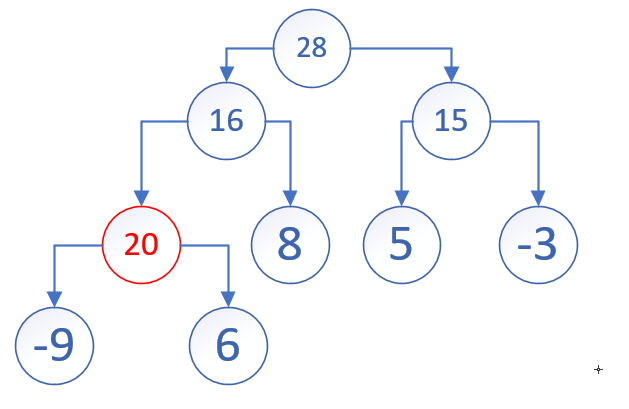
现在我们该开始考虑怎么维护性质了。注意到此时有两种情况:
新节点小于等于父节点
新节点大于父节点
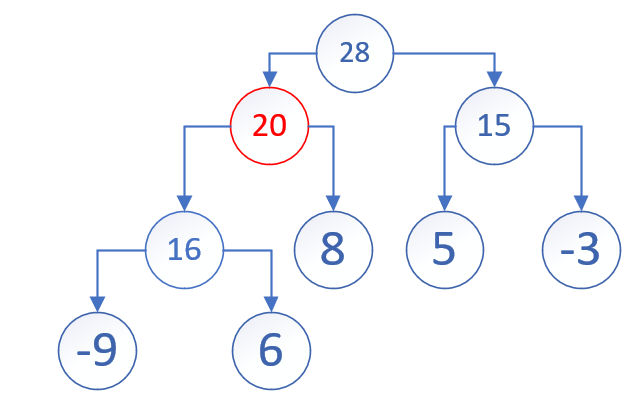
不过不要担心,我们只需要交换父节点与新节点,那么至少对于这颗子树而言,这个性质就成立了嘛! 只要我们交换,道路就会不断延伸。所以,不要停下来啊!
于是,我们成功维护了它的性质!
1 2 3 4 5 6 7 8 9 10 11 12 13 void push (ValueT data) m_data.push_back (data); m_size++; size_t now=m_size; size_t fa=now/2 ; while (fa!=0 &&!cmp (m_data[now],m_data[fa])) { std::swap (m_data[now],m_data[fa]); now=fa; fa=now/2 ; } }
删除
的确,我们可以直接删除根节点。但是……这样就把一棵树分成两颗了喂!QAQ
而且,数组中删除首元素也不是特别简单的。
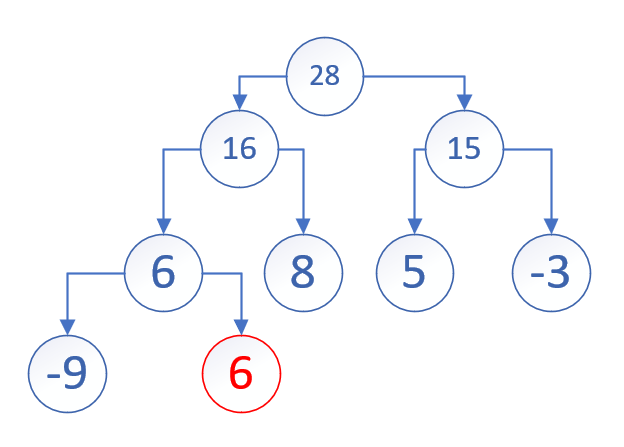
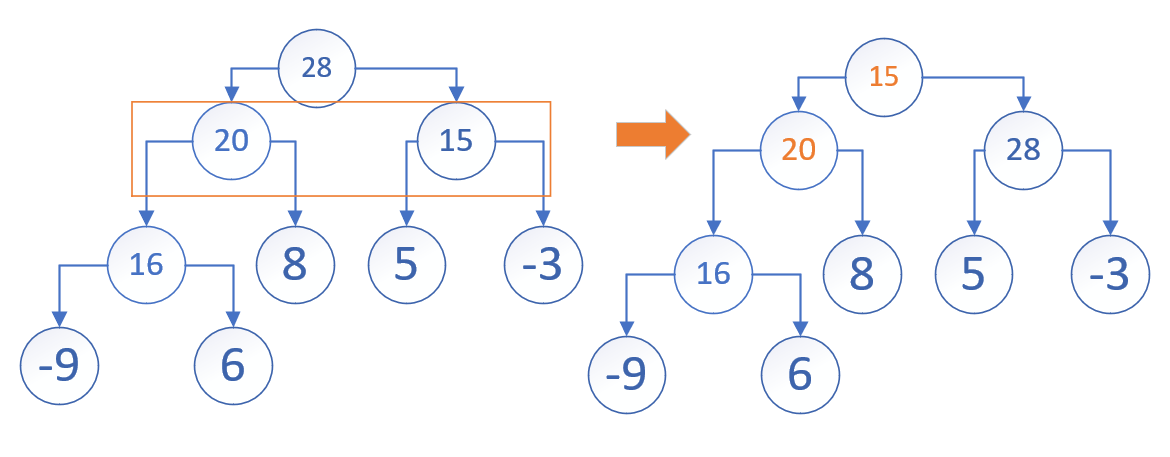
对此,我们能不能把插入反过来,把根节点慢慢移到最后面,然后直接pop_back就完事了嘛!
但是实际上……这么搞也不太得行。因为你想要移到最后面,必然和右节点交换。万一右节点小于左节点了咋整?遇到困难睡大觉
对此,我们不妨来找一个“替罪羊”。就决定是你了!最后一个节点!
1 2 std::swap (m_data[1 ],m_data[m_size]); m_data.pop_back ();
对此,我们找到这个新堆的左右两个子节点中较大的那一个,然后不断与其交换直到满足性质即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void pop () std::swap (m_data[1 ],m_data[m_size]); m_data.pop_back (); m_size--; size_t now=1 ; while (now*2 <=m_size) { size_t p=now*2 ; if (now*2 +1 <=m_size&&cmp (m_data[now*2 ],m_data[now*2 +1 ])) { p=now*2 +1 ; } if (!cmp (m_data[now],m_data[p])) { break ; } std::swap (m_data[now],m_data[p]); now=p; } }
复杂度
对于一个完全二叉树,当其有n个节点时,层数为log(n)层。O ( 1 ) O(1) O ( 1 ) O ( l o g ( n ) ) O(log(n)) O ( l o g ( n ))
附加:建堆
对于建堆过程,一个一个插入需要O ( n l o g n ) O(nlogn) O ( n l o g n ) O ( n ) O(n) O ( n )
完整代码&&验证
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 #pragma once #include "../queue.hpp" #include <cstddef> #include <functional> #include <utility> namespace my_lib{ template <typename ValueT, typename Container = deque<ValueT>, class Comp = std::less<ValueT>> class heap{ public : private : Container m_data; size_t m_size; Comp cmp; public : heap () { m_data.push_back (0 ); } heap (std::initializer_list<ValueT> init) { m_data.push_back (0 ); for (auto i : init) { push (i); } } template <class InitCont > heap (InitCont init) { m_data.push_back (0 ); for (auto i : init) { push (i); } } heap (const heap &rhs) { m_data = rhs.m_data; m_size = rhs.m_size; } heap (heap &&rhs) { m_data = rhs.m_data; m_size = rhs.m_size; } heap &operator =(const heap &rhs) { m_data = rhs.m_data; m_size = rhs.m_size; return *this ; } heap &operator =(const heap &&rhs) { m_data = rhs.m_data; m_size = rhs.m_size; return *this ; } public : size_t size () { return m_size; } ValueT top () { return m_data[1 ]; } void push (ValueT data) { m_data.push_back (data); m_size++; size_t now = m_size; size_t fa = now / 2 ; while (fa != 0 && !cmp (m_data[now], m_data[fa])) { std::swap (m_data[now], m_data[fa]); now = fa; fa = now / 2 ; } } void pop () { std::swap (m_data[1 ], m_data[m_size]); m_data.pop_back (); m_size--; size_t now = 1 ; while (now * 2 <= m_size) { size_t p = now * 2 ; if (now * 2 + 1 <= m_size && cmp (m_data[now * 2 ], m_data[now * 2 + 1 ])) { p = now * 2 + 1 ; } if (!cmp (m_data[now], m_data[p])) { break ; } std::swap (m_data[now], m_data[p]); now = p; } } }; };
验证