前言

由于这个学期选了一节硬件设计的课程，所以开始写一些硬件的小东西w

所以不妨从一个最核心也比较简单的部件：加法器开始？

我默认你对二进制已经很熟悉惹。不熟悉的话，可以去看一些进制相关的内容？

全加器

如果你对这些内容已经很熟悉的话，跳转到相应的区域吧！

半加器

要想谈论更多位的加法器，我们不妨先来看看一位得到加法器是怎么构成的w
不妨设其输入的两个值为A和B，输出S和进位C（正如你10进制下单位的加法也会有进位一样！）
或许你会想到画一个真值表，但……我们不妨直接来想想吧。

什么时候S会为1呢？当A和B同时为1时？不是，因为此时进位了，S为0。A和B同时为0呢？也不行，0+0=0。也就是说，当且仅当A和B中只有一个为1时，S才为1。也就是如下表示：

1
S=(A&!B)|(!A&B);

在这里，我们不妨约定下记号。和C语言中类似，&代表按位与，|代表按位或，!代表按位非，^代表按位异或。注意里面并没有同或，当我们必须用到时使用!(A^B)代替。

由于有公式：(A&!B)|(!A&B) == (A^B)，上面的代码更好写为：

1
S=A^B;

类似的，我们可以得到，当且仅当A和B同时为1，C为1。也就是：

1
C=A&B;

于是我们就得到了半加器的代码！

1
2
3
4
5
6
7
8
9
module half_adder(
    input wire A,
    input wire B,
    output logic S,
    output logic C
);
    assign S = A ^ B;
    assign C = A & B;
endmodule

如果你不懂Verilog语法的话……不用慌！你可以先不用去学，毕竟代码还是很直观的。

但是……老实说，半加器不太有用。毕竟……现实中输入肯定还有前一位的进位吧！所以我们需要：

全加器

全加器就是带上进位的加法器！其输入为A，B，Ci，输出S和Co。Ci为上一位的进位。

既然之前我们用脑子直接得到了公式，这里我们不妨使用一下真值表吧？（因为之后我们都不会用到了，让我们怀念一下它）

A B Ci S Co
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

不难注意到！

1
2
S=A^B^Ci;
C=(A&B)|(A&Ci)|(B&Ci);

如果您理解了之前半加器的公式，这里应该是很清晰的！（也就是S当且仅当A或B或Ci中有一个为1或同时为1时。第一个异或相当于计算A+B，第二个异或计算(A+B)+C（进位舍去））

完整代码如下：

1
2
3
4
5
6
7
8
9
10
module full_adder(
    input wire A,
    input wire B,
    input wire Ci,
    output logic S,
    output logic Co
);
    assign S = A ^ B ^ Ci;
    assign C = (A & B) | (A & Ci) | (B & Ci);
endmodule

我们看看生成的全加器长什么样吧w
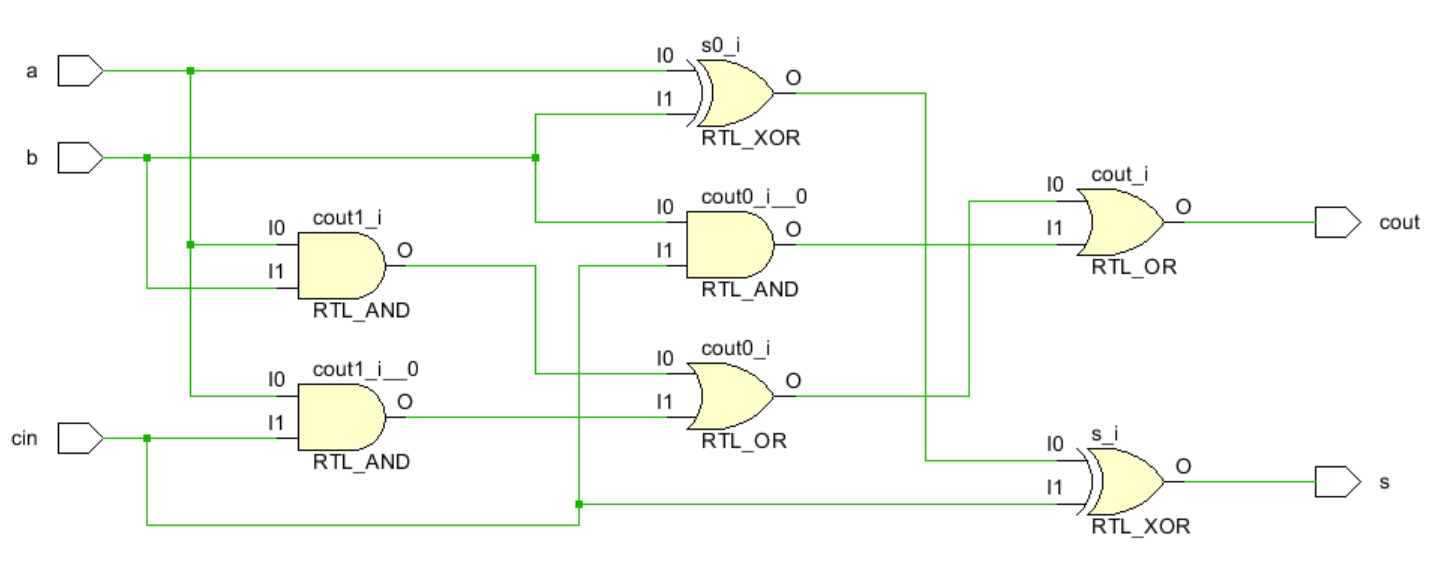
全加器结构

纹波进位加法器

全加器：这是我最后的波纹啦！（大雾

既然我们已经能做到每位的加法和进位处理了，只要把它们串联起来，是不是就可以生成多位的加法器了呢？

答案是肯定的！我们来试一个四位的加法器吧w

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
    input wire[3:0] A,
    input wire[3:0] B,
    output logic[3:0] S,
    output logic C
);
    wire[4:0] carry;
    assign carry[0]=0;
    full_adder adder0(
        .A(A[0]),
        .B(B[0]),
        .Ci(carry[0]),
        .S(S[0]),
        .Co(carry[1])
    );
    full_adder adder1(
        .A(A[1]),
        .B(B[1]),
        .Ci(carry[1]),
        .S(S[1]),
        .Co(carry[2])
    );
    full_adder adder2(
        .A(A[2]),
        .B(B[2]),
        .Ci(carry[2]),
        .S(S[2]),
        .Co(carry[3])
    );
    full_adder adder3(
        .A(A[3]),
        .B(B[3]),
        .Ci(carry[3]),
        .S(S[3]),
        .Co(carry[4])
    );

    assign C=carry[4];
endmodule

对于调用其它模块，你可以理解为：.X(Y)就是将线Y与模块中的X相连。当然……要是你更喜欢编程语言的话，不妨这么理解吧：把模块当成一个函数，这里便是给它传参；input将它的值放了进去，output传入了它的引用（也就是内部变量更改时，外部的变量也会相应更改）。但是这里有点小区别：对于硬件来说，所有的计算都是同时进行，几乎同时完成的，而不是顺序执行的。（不过你要是不理解的话…目前按老办法也不是不行）。

我们来看看它长什么样吧w

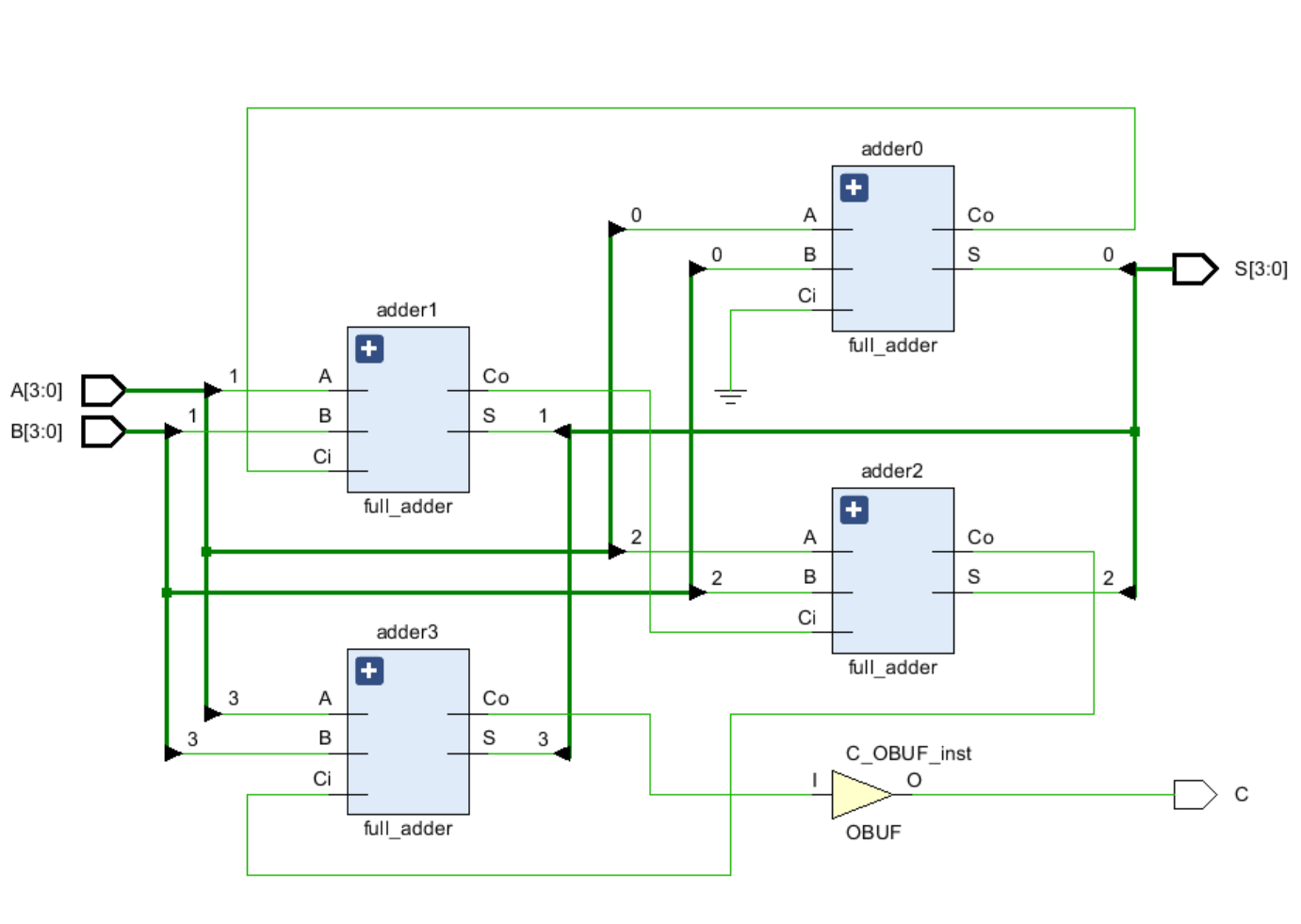
4位全加器

需要注意！这里仿真软件实际上是把结构重排以便节省空间了。如果你注意观察的话，会发现：每一位的Ci实际上都依赖于前一位的Co！也就是，直观的结构应该是下面这个样子：（取消了bundle nets）

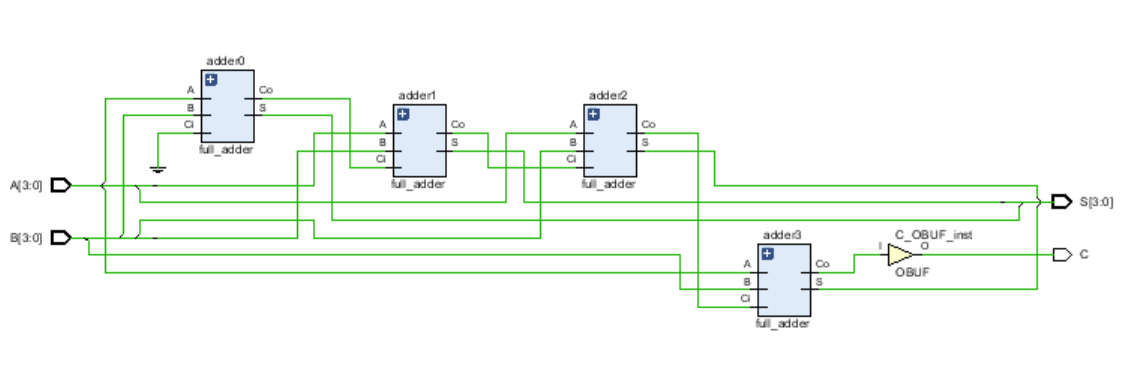
4位全加器_2

姆……它能用，但是……就是有点长。那如果64个连起来的话……

好吧你要是一个个手写也不是不可以（让我想起了那个1万多行的狠人）……我们可能需要一些循环的定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
module adder_64(
    input wire[63:0] A,
    input wire[63:0] B,
    output logic[63:0] S,
    output logic C
);
    wire[64:0] carry;
    assign carry[0]=0;

    genvar i;
    generate for (i=0;i<64;i=i+1) 
        begin:FOR
            full_adder adder(
                .A(A[i]),
                .B(B[i]),
                .Ci(carry[i]),
                .S(S[i]),
                .Co(carry[i+1])
            );
        end
    endgenerate
    assign C=carry[64];
endmodule

让我们来看看它长什么样吧。

64位加法器

呃……呃……呃……（救命（小声））

里面每个几像素的方框就是一个全加器。
好趴，它至少能正常运行……（这也太长了吧喂！）

但是……我们必须来谈谈房间里的那头大象了。（什么奇怪的直译！）
还记得我上面说的是

几乎同时输出

吗？
因为你仔细想一想，电路中每个门运算也是需要一点点时间的，所以如果经过的门越多，则其输出所需的时间越长。在之前，我们的还不算太长，所以可以暂时忽略这点。但是现在……有点过于长惹。

我们可以来计算一下（也可以跳过，知道时间很长就行了！）

每个全加器都由三层门电路组成（可以去看之前全加器的结构图），我们不妨假设每层门电路都需要 TT 的时间完成运算，那么64层全加器就是…… 64∗3∗T=192∗T64 * 3 * T = 192 * T的时间。

在低速或者你不想管性能时，那再长也不用管。但是如果你想让运算速度（主频）快一些的话，那降低延迟就是必不可少的了。

那……有没有办法解决这件事呢？

门电路啊，全加器的能力是有极限的。我从这短暂的硬件编写中，学到一件事：全加器连的越长，反而越容易陷入意想不到的困境，前功尽弃，除非超越全加器。我不用全加器了！我要超越延迟！

超前进位加法器

我们发现，延迟主要出现在进位的过程中。那么，我们能不能提前算出进位呢？

姆……让我们来试试：

1
2
3
C[1] = (A[0] & B[0]) | (A[0] & C[0]) | (B[0] & C[0]);

C[2] = (A[1] & B[1]) | (A[1] & C[1]) | (B[1] & C[1]);

让我们把C[1]扩展进去：

1
C[2] = (A[1] & B[1]) | (A[1] & (A[0] & B[0]) | (A[0] & C[0]) | (B[0] & C[0])) | (B[1] & (A[0] & B[0]) | (A[0] & C[0]) | (B[0] & C[0]));

我们发现其中A[x]&B[x]似乎很常见，我们不妨令g=A&B（为什么叫g后面再说）
等等……似乎还可以化简！只要我们把C[0]提出来的话……

1
2
C[1] = g[0] | (A[0] & C[0]) | (B[0] & C[0]);
C[1] = g[0] | ((A[0] | B[0]) &C[0] );

欸嘿……我们似乎又找到一个结构：A[x]|B[x]（如果你没发现的话，把C[2]的也写出来吧？下面就有（趴 ）

那我们就有：

1
2
3
4
5
6
7
8
9
10
C[1] = g[0] | (p[0] & C[0]);

C[2] = g[1] | ((A[1] | B[1] ) & C[1]);
C[2] = g[1] | (p[1] & g[0]) | (p[1] & p[0] & C[0]);

//让我们省略一些化简步骤
C[3] = g[2] | (p[2] & g[1]) | (p[2] & p[1] & g[0]) | (p[2] & p[1] & p[0] & C[0]);

//我们似乎找到规律了！让我们直接写出C[4]吧！
C[4] = g[3] | (p[3] & g[2]) | (p[3] & p[2] & g[1]) | (p[3] & p[2] & p[1] & g[0]) | (p[3] & p[2] & p[1] & p[0] & C[0]);

我们发现：仅需要两层我们就能计算出4位的进位了！
那么我们能不能直接算出64位的进位呢？

理论可行，但实际中……且不说这么多输入的门能不能造出来，其不稳定性和复杂度也会成倍增加。所以，我们一般就使用4位最多啦。

我们把这么一个模块称为CLA（Carry Look-Ahead，前瞻进位）。其代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
module CLA (
    input wire[3:0] A,
    input wire[3:0] B,
    input wire C,
    output logic[3:0] O,
    output logic P,
    output logic G
  );
  wire[3:0] p;
  wire[3:0] g;

  assign p=A|B;
  assign g=A&B;

  assign O[0]=g[0]|(p[0]&C);
  assign O[1]=g[1]|(p[1]&g[0])|(p[1]&p[0]&C);
  assign O[2]=g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&C);
  assign O[3]=g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&p[1]&p[0]&C);

  assign P=p[3]&p[2]&p[1]&p[0];
  assign G=g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0]);
endmodule

（为什么需要输出P和G让我们之后再谈。

那，要是我们不满足于4位呢？我们想要8位呢？

由于每个CLA都需要上一个CLA进位的值……当然我们可以串联起来，然后就此满足。

但……可以继续并行下去吗？

答案是肯定的！我们可以嵌套使用CLA。我们把CLA的CLA叫做BCLA（Batch，批）吧！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
module BCLA (
    input wire[15:0] A,
    input wire[15:0] B,
    input wire C0,
    output logic P,
    output logic G,
    output logic[15:0] O
  );
  wire C3,C7,C11;
  wire[3:0] p,g;

  CLA cla0(
        .A(A[3:0]),
        .B(B[3:0]),
        .C(C0),
        .O(O[3:0]),
        .P(p[0]),
        .G(g[0])
      );
  assign C3=g[0]|(p[0]&C0);

  CLA cla1(
        .A(A[7:4]),
        .B(B[7:4]),
        .C(C3),
        .O(O[7:4]),
        .P(p[1]),
        .G(g[1])
      );
  assign C7=g[1]|(p[1]&g[0])|(p[1]&p[0]&C0);

  CLA cla2(
        .A(A[11:8]),
        .B(B[11:8]),
        .C(C7),
        .O(O[11:8]),
        .P(p[2]),
        .G(g[2])
      );
  assign C11=g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&C0);

  CLA cla3(
        .A(A[15:12]),
        .B(B[15:12]),
        .C(C11),
        .O(O[15:12]),
        .P(p[3]),
        .G(g[3])
      );

  assign P=p[3]&p[2]&p[1]&p[0];
  assign G=g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0]);

endmodule

姆……你觉得这是不是依然是串联？只不过把串联封装起来了……

但是并不！这里用到了我们留下的两个伏笔：所有电路是同时运算的，我们输出了每一块最后的P、G值

也就是说：在第 1T1T 的时候，每个CLA就算出了自己的p、g值（注意到了吗？p、g是不依赖于最初的进位的）；第 2T2T 的时候，每个CLA就算出了传出的P、G值（P、G也是不依赖于进位的哦！）；第 4T4T 的时候，BCLA就算出了每个CLA模块的最初进位（也就是C3、C7、C11），并传回给了CLA；第 6T6T 的时候，CLA计算出了每一位的进位，并输出。

（当然如果你看不懂的话…先承认我们只需要 6T6T 就行啦）

也就是说，原本需要 3∗16∗T=48T3*16*T=48T 才能算出的进位值，我们仅用了 6T6T 就完成了。多棒啊这！

同时，我们发现BCLA和CLA是如此的相似…（只是要调用模块+计算进位罢了）。那我们把4个BCLA也这么组合起来，是不是就能得到64位的每个进位了捏？

答案是肯定的！让我们来试试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
module LBCLA (
    input wire[63:0] A,
    input wire[63:0] B,
    input wire C0,
    output logic[63:0] O,
    output logic P,
    output logic G
  );
  wire C15,C31,C47;
  wire[3:0] p,g;

  BCLA bcla0(
         .A(A[15:0]),
         .B(B[15:0]),
         .C0(C0),
         .O(O[15:0]),
         .P(p[0]),
         .G(g[0])
       );
  assign C15=g[0]|(p[0]&C0);

  BCLA bcla1(
         .A(A[31:16]),
         .B(B[31:16]),
         .C0(C15),
         .O(O[31:16]),
         .P(p[1]),
         .G(g[1])
       );
  assign C31=g[1]|(p[1]&g[0])|(p[1]&p[0]&C0);

  BCLA bcla2(
         .A(A[47:32]),
         .B(B[47:32]),
         .C0(C31),
         .O(O[47:32]),
         .P(p[2]),
         .G(g[2])
       );
  assign C47=g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&C0);

  BCLA bcla3(
         .A(A[63:48]),
         .B(B[63:48]),
         .C0(C47),
         .O(O[63:48]),
         .P(p[3]),
         .G(g[3])
       );



  assign P=p[3]&p[2]&p[1]&p[0];
  assign G=g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0]);
endmodule

（请不要问我为什么要叫LBCLA…我真的取不出名字惹）

所以，我们成功获得了64位每位的进位！而且时间非常非常短（比之前纹波进位的4位加法器还少哦！）

而最后我们算S，只需要将A、B与C异或起来就行了w。（也就是A+B+C）
（Co的话就是最后一个carry啦！）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
module ADDER_64 (
    input wire[63:0] A,
    input wire[63:0] B,
    input wire Ci,
    output logic Co,
    output logic[63:0] S
  );
  wire[64:0] C;
  wire p,g;
  LBCLA lbcla(
          .A(A),
          .B(B),
          .C0(Ci),
          .O(C[64:1]),
          .P(p),
          .G(g)
        );

  assign C[0]=Ci;

  assign S=A^B^C[63:0];
  assign Co=C[64];
endmodule

哦哦哦哦哦哦——我们成功惹qwq
快去仿真一下试试？qwq

一些理论

实际上，g被叫做进位生成因子，p被叫做进位传递因子。让我们想一想为什么公式是这样的？

如果这一位输入均为1（也就是g为1），则该位必然存在进位。否则的话，如果上一位存在进位且这一位有一个1（也就是p为1），则该位必然存在进位。发现这是什么的描述了吗？

1
C[0]=g[0]|(p[0]&C[0]);

那下一位呢？g是一样的，那么后面的公式呢？我们发现，其实就是把前面某一位的进位一个一个传过来了！
让我们以C[1]为例：

1
C[1]=g[1]|(p[1]&g[0])|(p[1]&p[0]&C[0])

其中，g[1]不再赘述；p[1]&g[0]为上一位的进位与这一位的某个1产生的进位；p[1]&p[0]&C[0]就是上上位给了进位到上一位，上一位又进位到了这一位。

以此类推……现在你应该模模糊糊感觉到为什么每个公式看起来如此规律了吧？因为它就是每次看前一位，一位一位传递过来的！

尾注

姆……其实最开始咱理解超前进位加法器也有点困难，无论是对于p、g的理解还是最后的结构为什么不是串行。不过在 ~抄~ 写代码的时候，慢慢摸索模模糊糊有了一点感觉。最后在撰写这篇博客的时候完全弄懂惹。

所以如果你还没明白的话，别急！去让它先跑起来测试一下，然后让它们慢慢沉淀吧。这样在某一天，说不定你就“啊哈！”一下恍然大明白了呢！

姆……这是这个系列文章的第一篇啦，之后应该还有几篇惹。