前言

在开始之前，我们必须要先谈谈我们的目标：
我们在这里并不是想完成一个大作业或者写出一个很好的乘法器，而是在你上完一天课后，在睡前的两小时内能完成的的一个作品。

所以，我并不会做出一个很好的乘法器，我们将会使用一些更简单的方式。
当然我知道，你肯定不会满足于此对吧？所以我们仍会谈一谈更快速乘法器的原理，并给出一点示例。

请一直记住这点吧：我们想要一个简单玩意，并尽可能的从中理解它的原理。

对了……你可能会发现，越往后面的内容其实越简单哦。所以实在不会的话，不要死磕哦w

那么w，让我们开始吧喵！

阵列乘法器

或许你已经学过计算机组成原理，并且脑子里已经充满了每次移位相加的东西（或者补码两位乘之类的）。
但是，还是让我们来看看吧。

我们不妨先从4位*4位的乘法开始：

对于以下的一个乘法：
$ 1011 * 0111 $

它是这么运算的：（希望格式是对的）

1
2
3
4
        1011    1
+      1011     1
+     1011      1
+    0000       0

（想一想10进制时，你是怎么做乘法的？）

它需要四个加法。我们可以这么做：（计组里为了节省空间，使用了两个寄存器并联。但是我们先不考虑w）
首先：拥有一个8bit的寄存器：

$ 00000000 $

接下来由于乘数第一个为1，高4位加上1011

$ 10110000 $

由于右移是左移的反操作，我们将这个数右移一位：

$ 01011000 $

重复以上步骤：

$ (1)00001000 $ 相加

$ 10000100 $ 移位

$ (1)00110100 $ 相加

$ 10011010 $ 移位

$ 10011010 $ 相加

$ 01001101 $ 移位

好的！我们算完惹~ 应该还是很简单的！只需要重复每次移位相加就行了。

但是……这样的话，一个XLEN*XLEN的乘法需要XLEN的周期。我们能不能优化一下？

答案是肯定的！毕竟，我们为什么不把4个16位的加法器串在一起使用呢？
也就是：

1
2
3
4
00001011 +
00010110 +
00101100 +
00000000 +

这种将多个加法器串联使用的，可以以延迟（和芯片面积）换周期。
但是，这样还不是完全的阵列加法器。因为，我们能发现：每次实际上只有四个数相加。所以，我们可以直接将后面的数输出就行了：

1
2
3
4
5
6
    x x x x 1 0 1 1
+   x x c 1 0 1 1 |
+   x c 1 0 1 1 | |
+   c 0 0 0 0 | | |
------------------------
    0 1 0 0 1 1 0 1

其中的c代表产生的进位。其画出来如下：（从某个地方偷了一张图过来（逃））
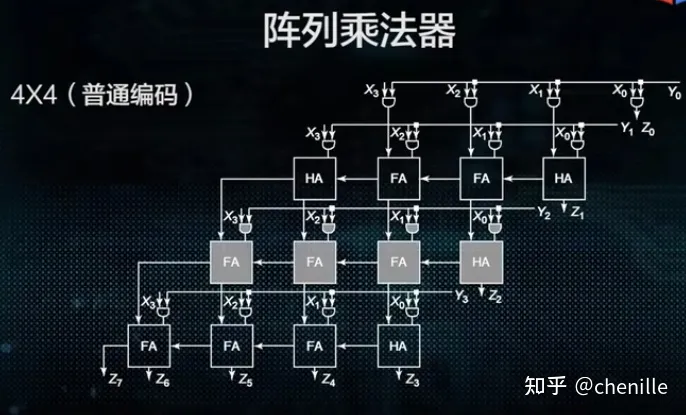
阵列加法器

当然注意到，它这里用的是纹波进位。你为什么不改成超前进位呢？

一点优化

即使这样，我们还是能发现，它依然是串行的结构。我们能不能引入一点并行呢？
答案是肯定的！我们可以先将前两位相加，再将后两位相加，最后再将结果相加：
也就是同时算（xxxx1011+xxx0110x）和（xx1011xx+x0000xxx）。需要注意的是，这里最后那个必须用16位加法器了！否则会丢掉进位哦。

1
2
3
4
5
00001011 \
00010110 - 00100001 \
                            01001101
00101100 - 00101100 /
00000000 /

其verilog代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
module MULER_16 (
    input wire[15:0] A,
    input wire[15:0] B,
    output logic[31:0] O
  );
  genvar i;
  //stg1
  wire[31:0] stg1[15:0];
  wire[15:0] pp0;
  assign pp0 = B[0] ? A :16'b0;
  assign stg1[0] = {16'b0,pp0[15:0]};
  generate
    for (i = 1; i<16 ; i=i+1 )
    begin:STG1
      wire[15:0] pp;
      assign pp = B[i] ? A : 16'b0;
      //   assign stg1[i][i+15:i] = pp[15:0];
      assign stg1[i][i+15:i] = pp[15:0];
      assign stg1[i][i-1:0] = 0;
      assign stg1[i][31:i+16] = 0;
    end
  endgenerate

  //stg2
  wire[31:0] stg2[7:0];
  generate
    for (i = 0;i< 8 ;i=i+1 )
    begin:STG2
      ADDER_32 adder(
                 .A(stg1[i*2]),
                 .B(stg1[i*2 + 1]),
                 .Ci(1'b0),
                 .S(stg2[i]),
                 .Co()
               );
    end
  endgenerate

  //stg3
  wire[31:0] stg3[3:0];
  generate
    for (i = 0;i<4 ;i=i+1 )
    begin:STG3
      ADDER_32 adder(
                 .A(stg2[i*2]),
                 .B(stg2[i*2 + 1]),
                 .Ci(1'b0),
                 .S(stg3[i]),
                 .Co()
               );
    end
  endgenerate

  //stg4
  wire[31:0] stg4[1:0];
  generate
    for (i = 0;i<2 ;i=i+1 )
    begin:STG4
      ADDER_32 adder(
                 .A(stg3[i*2]),
                 .B(stg3[i*2 + 1]),
                 .Ci(1'b0),
                 .S(stg4[i]),
                 .Co()
               );
    end
  endgenerate

  ADDER_32 adder_STG5(
             .A(stg4[0]),
             .B(stg4[1]),
             .Ci(1'b0),
             .S(O),
             .Co()
           );
endmodule

64位？

至此我们成功设计了一个阵列乘法器！这个原理同样可以拿来运算64位的乘法。也就是，先将64个64位的部分积并行相加，得到32个65位的部分积（注意进位！）；再将其并行相加，得到16个66位的部分积；再将其相加，得到8个67位的部分积…

看起来不错！你是想写这么多奇怪位数的加法器呢？qwq
或者直接使用一个128位的加法器呢？qwq

从小位宽到大位宽

但是……直接设计一个大位宽的乘法器对我们的睡眠并不是很友好。你想的话……可以早上再试试？所以，我们需要一些数学的帮忙。

容易注意到：（乘法分配律）

A[63:0]∗B[63:0]A[63:0] * B[63:0]

=(A[63:32]∗232+A[31:0])∗(B[63:32]∗232+B[31:0])= (A[63:32]*2^{32} + A[31:0]) * (B[63:32]*2^{32} + B[31:0])

=(A[63:32]∗B[63:32])∗264+(A[63:32]∗B[31:0])∗232+(A[31:0]∗B[63:32])∗232+(A[31:0]∗A[31:0])= (A[63:32] * B[63:32])*2^{64} + (A[63:32] * B[31:0])*2^{32} + (A[31:0] * B[63:32])*2^{32} + (A[31:0] * A[31:0])

=(A[63:32]∗B[63:32])<<64+(A[63:32]∗B[31:0])<<32+(A[31:0]∗B[63:32])<<32+(A[31:0]∗A[31:0])= (A[63:32] * B[63:32]) << 64 + (A[63:32] * B[31:0]) << 32 + (A[31:0] * B[63:32]) << 32 + (A[31:0] * A[31:0])

所以，两个64位数的乘法可以由4个32位乘法器得到；更低位的以此类推……

在这里我不得不提到一个一直被忽略的问题：两个64位相乘是128位的，但是我们总不能专门写一个128位的加法器吧。对此，RISCV64-M给出的答案是：有一条指令输出它的低位，另一条指令输出它的高位。（如果你更熟悉x86-64的话，它是符号位扩展，并分别放入rax和rdx中）。也就是，我们并不需要一个128位的加法器；我们拼接一下更好。

所以我们能有以下的代码（按照RISCV，每次只输出高/低位）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
module MULER_64_U (
    input wire[63:0] A,
    input wire[63:0] B,
    input wire IS_LOW,
    output logic[63:0] O
  );

  wire[63:0] L,M1,M2,H;
  MULER_32 mul0(
             .A(A[31:0]),
             .B(B[31:0]),
             .O(L)
           );
  MULER_32 mul1(
             .A(A[31:0]),
             .B(B[63:32]),
             .O(M1)
           );
  MULER_32 mul2(
             .A(A[63:32]),
             .B(B[31:0]),
             .O(M2)
           );
  MULER_32 mul3(
             .A(A[63:32]),
             .B(B[63:32]),
             .O(H)
           );
  wire[63:0] LP,HP,MP;
  wire Cm,Cl;

  ADDER_64 adder_m(
             .A(M1),
             .B(M2),
             .Ci(1'b0),
             .S(MP),
             .Co(Cm)
           );

  ADDER_64 adder_l(
             .A(L),
             .B({MP[31:0],32'b0}),
             .Ci(1'b0),
             .S(LP),
             .Co(Cl)
           );

  ADDER_64 adder_h(
             .A(H),
             .B({31'b0,Cm,MP[63:32]}),
             .Ci(Cl),
             .S(HP),
             .Co()
           );

  assign O = IS_LOW ? LP : HP;
endmodule

事实上，我们已经可以就用这个乘法器然后说乌拉啦！
（32位的乘法器相信你能用同样的思路很快写出来）

有符号乘法？

虽然之前一直在忽略，但到这里，我们不得不提一下房间里的一只大象了：之前我们一直在进行的是无符号数的乘法，但是现实中却经常是有符号数的乘法。

或许你已经开始想补码的乘法了（之后会提一句）。但是，这并不是我们这章的重点。同时我们现在应该已经够困惹，所以让我们快速的用个简单方法搞定吧。
那就是，直接将负数转为它的绝对值，最后乘完后添上符号就行了。

将负数变为绝对值的方法就是：全部取反加一！（包括符号位）

需要注意的是……有符号数可以与无符号数相乘，最终的结果为有符号数。这部分可以看这里：RISCV-ISA section7.1

最终的组合应该不是很难（主要就是处理符号和位数啦）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
module MULER_64 (
    input wire[63:0] A,
    input wire[63:0] B,
    input wire SIGA,
    input wire SIGB,
    input wire IS_LOW,
    output logic[63:0] O
  );
  wire[63:0] a,b;
  wire[63:0] absa,absb;

  wire is_neg,is_unsigned;

  ADDER_64 adder64_0(
             .A(~A),
             .B({64'b0}),
             .Ci(1'b1),
             .S(absa),
             .Co()
           );
  ADDER_64 adder64_1(
             .A(~B),
             .B({64'b0}),
             .Ci(1'b1),
             .S(absb),
             .Co()
           );

  assign is_neg = (SIGA&~SIGB&A[63])|(~SIGA&SIGB&B[63])|(SIGA&SIGB&(A[63]^B[63]));
  assign is_unsigned=~(SIGA|SIGB);

  assign a = !SIGA ? A :
         A[63]? absa:
         A;

  assign b = !SIGB ? B :
         B[63]? absb:
         B;

  wire[63:0] res;
  MULER_64_U multr_64_u(
               .A(a),
               .B(b),
               .IS_LOW(IS_LOW),
               .O(res)
             );

  wire[63:0] nres;
  ADDER_64 adder64_2(
             .A(~res),
             .B({64'b0}),
             .Ci(1'b1),
             .S(nres),
             .Co()
           );

  assign O = (is_unsigned ) ? res :
         (!is_neg & IS_LOW) ? res :
         (!is_neg & !IS_LOW) ? {1'b0,res[62:0]} :
         (is_neg & IS_LOW) ? nres :
         (is_neg & !IS_LOW) ? {1'b1,res[62:0]} :
         res;
endmodule

好了！我们现在已经成功实现一个乘法器惹！快去仿真试试吧！

如果你还有时间改造一下的话……可以再看看下面的内容，它可以让这个乘法器跑得更快。
但是如果你不想的话，直接跳到文章末尾也是可以的哦.

下面这一部分可以跳过哦

bonus: wallance树 和 CSA

注意到，我们之前的阵列乘法器中，使用了大量的加法器。虽然超前进位加法器是很快啦……但是在大位宽的情况下，延迟依然偏高。有没有办法改进一下这一点捏？

让我们来想想……似乎在吞进两个数，吐出一个数这件事上，我们已经没法达到更优了。我们看起来需要换一条赛道。

那……吞进三个数吐出两个数呢？嗯……有意思，让我们来看看。

CSA：进位保留加法器

吞进三个数，吐出两个数的话，我们需要先想想吐出来的是什么。总不能是随机选两个数吧！

我们不妨先想想，还有什么东西是吞进一个东西，吐出两个东西。最后把这两个东西相加后还能得到正确值？不知道你想到了没有，这里公布答案吧：全加器。

它输出两个东西是容易理解的。但是，为什么两个输出相加为正确值呢？这里需要看看我们上次所说的超前进位加法器。注意到，当我们算出所有的进位时，我们做了这样一件事：S = (A^B^C)。相当于第一部分的输出是 M=(A+B)M = (A+B) ，然后又计算了 S=(M+C)S = (M+C)。

于是，我们能用一堆全加器构成一层，每一层都能消去一个数。
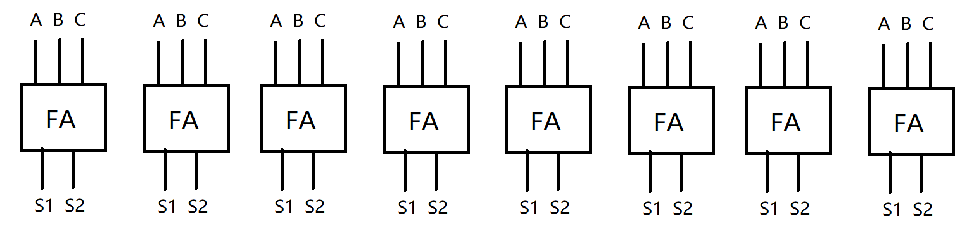
CSA（一层）
同时，每一层内都是全并行的。

这可比每次用64位全加器消去一个数快多了！（并且更容易构建不同位数的加法）

这里是它的Verilog代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
parameter XLEN;
module CSA32(
    input wire[XLEN-1:0] A,
    input wire[XLEN-1:0] B,
    input wire[XLEN-1:0] C,
    output logic[XLEN-1:0] S1,
    output logic[XLEN-1:0] S2
);
    genvar i;
    generator
        for ( i = 0; i < XLEN ; i = i + 1)
        begin: CLA
            full_adder adder(
                .A(A[i]),
                .B(B[i]),
                .Ci(C[i]),
                .S(S1[i]),
                .Co(S2[i])
            );
        end
    endgenerator
endmodule

wallance树

于是，与刚才我们用一堆全加器并行一样的，我们可以用一堆CSA并行。为了表示这种并行关系，我们可以画出一棵树：
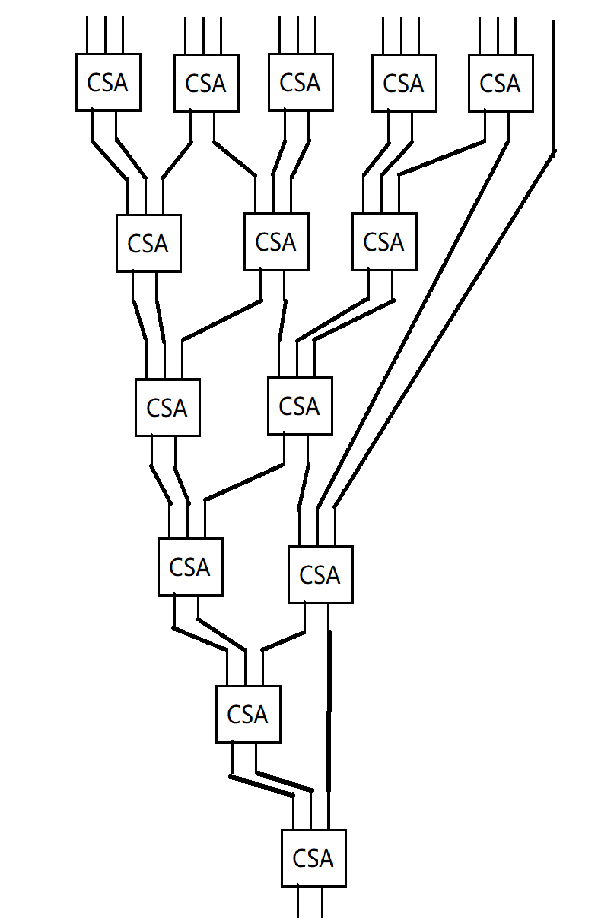
wallance树
（孩子用触控板画的，别骂了）
这看起来层数比前面的多多了，不是吗？（前面的层数是log2XLENlog_{2}{XLEN}，也就是16个数相加需要4层）但是，我们需要注意到，这里每一层的延迟都大大减小了，所以总体上是更有利的。

然而我们容易发现……由于我们的加数总是2n2^n，3-2对于我们来说并不是太好设计。所以现实中，我们可能会采用4-2的CSA。
但是姆……它有亿点复杂，其结构如下：
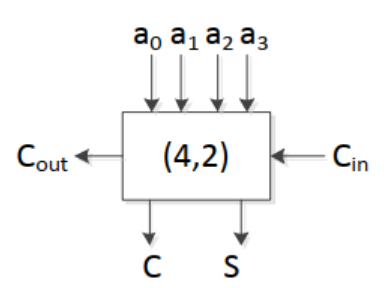
4-2CSA

注意到，这时每个单元必须依赖前一位的进位了。

还记得我们在文章开头讲的吗？我们会采用一些更简单的方式，而不是死磕某个难点。（我们还要睡觉呢！）

所以，请允许我直接给你一个代码吧。看不懂就先不用管啦~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
parameter XLEN;
module CSA42(
    input wire[XLEN-1:0] A,
    input wire[XLEN-1:0] B,
    input wire[XLEN-1:0] C,
    input wire[XLEN-1:0] D,
    input wire Ci,
    output logic[XLEN-1:0] S1,
    output logic[XLEN-1:0] S2,
    output wire Co
);
    input   [length*2-1 : 0]  in1,in2,in3,in4;
    input                     cin;
    output  [length*2 : 0]  out1,out2;
    output                    cout;
    wire    [XLEN-1:0]  w1,w2,w3;

assign w1 = A ^ B ^ C ^ D;
assign w2 = (A & B) | (C & D);
assign w3 = (A | B) & (C | D);

assign S2 = { w1[XLEN-1] , w1} ^ {w3 , Ci};
assign Co = w3[length*2-1];
assign S1 = ({ w1[XLEN-1] , w1} & {w3 , Ci}) | (( ~{w1[XLEN-1] , w1}) & { w2[XLEN-1] , w2});

endmodule

bonus: 布斯乘法器

我们发现，上面的操作本质上是在不断的将一堆数相加。这里我们不妨专业点，把这些数叫做“部分积”。也就是说，我们进行乘法的时间与部分积的个数密切相关。

那，有没有办法消除部分积的个数呢？容易注意到，当乘数的某一位是0的时候，其实就相当于没有这个部分积了。也就是说，我们希望里面的0越多越好。有什么办法吗？

需要注意的是，我们这里讲的是基四布斯乘法，计组课本上可能叫做补码两位乘。类似的，还有基五乘法、基七乘法等等。

我们需要来进行一些数学上的推导（注意这里都是有符号数哦）：

一般的，一个二进制数可以被表示为：

$ y= -2^{n-1}y_{n-1} + \sum_{i=n-2}^{0}2^{i}y_{i} $

不失一般性的，我们可以在后面加上一位：

$ y= -2^{n-1}y_{n-1} + \sum_{i=n-2}^{0}2^{i}y_{i} + y_{-1} \text{ , where } y_{-1} = 0 $

我们将公式展开，不容易注意到：

$ y= -2^{n-1}y_{n-1} + 2^{n-2}y_{n-2} + 2^{n-3}y_{n-3} + \dots + 2^{2}y_{2} + 2^{1}y_{1} + 2^{0}y_{0} + y_{-1}  \ = -2^{n-1}y_{n-1} + 2^{n-2}y_{n-2} \red{+ 2^{n-2}y_{n-2} - 2^{n-2}y_{n-2}} + 2^{n-3}y_{n-3} \red{+ 2^{n-3}y_{n-3} - 2^{n-3}y_{n-3}} + \dots + 2^{1}y_{1} \red{+ 2^{1}y_{1} - 2^{1}y_{1}} + 2^{0}y_{0} \red{+ 2^{0}y_{0} - 2^{0}y_{0}} + y_{-1}  \ = -2^{n-1}y_{n-1} + \blue{2^{n-1}y_{n-2}} - \red{2^{n-2}y_{n-2}} + \blue{2^{n-2}y_{n-3}} - \red{2^{n-3}y_{n-3}} + \dots + \blue{2^{2}y_{1}} - \red{2^{1}y_{1}} + \blue{2^{1}y_{0}} - \red{2^{0}y_{0}} + y_{-1}  \ = 2^{n-1}\blue{(-y_{n-1} + y_{n-2})} + 2^{n-2}\blue{(-y_{n-2} + y_{n-3})} + \dots + 2^{2}\blue{(-y_{2} + y_{1})} + 2^{1}\blue{(-y_{1}+y_{0})} + 2^{0}\blue{(-y_{0} + y_{-1})} $

易知，这么做可以将相邻项都为1时变为0，这样，我们成功增加了0的个数。但是，这并没有显著减少部分积的个数。（非常建议自己抄一遍）

让我们继续，将上面第二个式子扩展，有：

$y = \red{-2}*2^{n-2}y_{n-1} + \red{2}2^{n-2}y_{n-2} + \red{22^{n-4}}y_{n-3} - 2^{n-3}y_{n-3} + \dots + \red{2}2^{1}y_{1} - \red{22^{0}}y_{1} + 2^{0}y_{0} + y_{-1} $

$y = -\red{22^{n-2}}y_{n-1} + \red{2^{n-2}}y_{n-2} + \red{2^{n-2}}y_{n-3} - \red{22^{n-4}}y_{n-3} + \red{2^{n-4}}y_{n-4} + \red{2^{n-4}}y_{n-5} + \dots + -22^{2}y_{3} + 2^{2}y_{2} + 2^{2}y_{1} - 22^{0}y_{1} + 2^{0}y_{0} + 2^{0}y_{-1}  \ y = 2^{n-2}(-2y_{n-1} + y_{n-2} + y_{n-3}) + 2^{n-4}(-2y_{n-3} + y_{n-4} + y_{n-5}) + \dots + 2^{2}(-2y_{3} + y_{2} + y_{1}) + 2^{0}(-2y_{1} + y_{0} + y_{-1}) $

此时，多项式的项数变为原来的一半，也就是部分积变为了一半。

$n-2,n-4,n-6 \dots $

对此，我们可以根据下表算出每个部分积：

x2i+1x_{2i+1} x2ix_{2i} x2i−1x_{2i-1} PPiPP_{i}
0 0 0 0
0 0 1 Y
0 1 0 Y
0 1 1 Y<<1
1 0 0 -Y<<1
1 0 1 -Y
1 1 0 -Y
1 1 1 0

而对于为什么要使用基四而不使用更高基，这是因为基四是唯一可以用移位算出部分积的。

我们有以下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
module booth (
    input wire[63:0] A,
    input wire[63:0] B,
    input wire SIGA,
    input wire SIGB,
    output logic[65:0] PP[32:0]
);
    wire[1:0] a_sig = SIGA ? {2{A[63]}} : 2'b00; 
    wire[1:0] b_sig = SIGB ? {2{B[63]}} : 2'b00; 

    wire[65:0] a = {a_sig, A};
    wire[65:0] na = ~a + 1;
    wire[65:0] a2 = a << 1;
    wire[65:0] na2 = na << 1;

    wire[65:0] b = {b_sig, B}; 

    genvar i;
    generate
        for (i=0;i<66;i=i+2)
        begin: BOOTH_PP
            assign PP[i/2] = (b[i+2:i] == 3'b001 || b[i+2:i] == 3'b010) ? a :
                             (b[i+2:i] == 3'b101 || y[i+2:i] == 3'b110) ? na   :
        	                 (b[i+2:i] == 3'b011) ? a2   :
        	                 (b[i+2:i] == 3'b100) ? na2 : 66'b0;
        end
    endgenerate
end

而后使用前面讲过的方法进行运算即可。

等等，为什么会把63位的输入变为65位呢？这是因为布斯乘法必须作用于有符号数，对于无符号数需要进行扩展变为有符号数才能正常运算。

那，我们前面为什么不使用布斯乘法呢？一是我们需要高低位分开，二是33个部分积……没法并行，必须一个个算，就很麻烦惹。

但是结合前面的方法，本质上布斯只是对部分积进行了一个转化而已，其余的部分都是一样的。

那除法呢？

很抱歉……除法比乘法难上一百倍……（单周期下）。所以我们要么引入多周期算除法，要么像个聪明的办法来解决。

注意到，64位整数本质上是一个模2642^64的群，该群位加法群和乘法群，拥有单位元。也就是对于每个数（除了0），都存在一个对应的数，使得：

$ (a * b) \equiv 1 \mod 2^{64} $

我们不妨称这个数为a−1a^{-1}

也就是，对于a/ba/b，我们可以计算

a∗b−1≡a/bmod  264a * b^{-1} \equiv a/b \mod 2^{64}

也就是，我们并不需要除法器？（如果我们的程序足够聪明的话）

关于更多的知识和如何求解逆元，详见：乘法逆元

尾注

说句实话……乘法比加法难。毕竟幼儿园都会的加法，可能小学高年级才学乘法。

而…计组教的确实也不是很好。明明在说原理，却总是又节省寄存器又多周期又标志位…实际上在学习的时候就应该往大了摊在优化？

毕竟咱最开始布斯乘法和CLA、wallance树这两部分也是看的头大……

不过相信……看完这篇再结合一些自己抄编写的代码，可以显著提高认识。

实际上，我们现在已经完成了ALU中最难的部分：计算！接下来，我们或许可以一口气讲完ALU惹w

喵喵喵qwq

那么，祝你的旅程愉快！(●’◡’●)

我们下一章见。